3.1. Mathematische Grundlagen

Im Folgenden wollen wir die mathematischen Grundlagen zur Untersuchung von allgemeinen Optimierungsproblemen einführen. Wir beginnen mit einigen Notationen.

Definition 3.1 (Notationen)

Wir fassen \(x\in\R^n\) grundsätzlich als Spaltenvektoren auf. Für eine stetig differenzierbare Funktion \({f:\R^n\to\R}\) bezeichnen wir mit

\[\nabla f(x) = f^\prime(x)^\top = \left( \frac{\partial f}{\partial x_1}(x), \ldots, \frac{\partial f}{\partial x_n}(x) \right)^\top\in\R^n\]

den Gradienten von \(f\) im Punkt \(x\). Insbesondere ist der Gradient ein Spaltenvektor. Für den Fall, dass \(f\) zweimal stetig differenzierbar ist, bezeichnen wir mit

\[\nabla^2 f(x) = \left( \frac{\partial^2 f}{\partial x_i \partial x_j} \right)_{i,j}\in\R^{n\times n}\]

die (symmetrische) Hessematrix von \(f\) im Punkt \(x\).

Zuletzt führen wir für vektorwertige Funktionen \({f:\R^n\to\R^m}\) die Schreibweise

\[f(x) \le 0 \quad\Longleftrightarrow\quad f_i(x) \le 0 \quad \text{für alle }i=1,\ldots,m\]

ein. Ausdrücke wir \({f(x)<0}\) oder \(h(x)=0\) sind also komponentenweise zu verstehen.

Damit lässt sich bereits das allgemeine Optimierungsproblem formulieren.

Definition 3.2 (Allgemeines Optimierungsproblem)

Sei \(\Omega \subset \mathbb{R}^n\) und sei \({f : \Omega \to \mathbb{R}}\) eine reellwertige Funktion, welche wir Zielfunktion nennen. Unser Ziel ist es, einen unbekannten Vektor \(x \in \Omega\), auch Parametervektor oder Designvektor genannt, zu finden, welcher das folgende allgemeine Optimierungsproblem löst:

(3.1)\[\begin{split}\begin{split} \min_{x\in\Omega} \quad & f(x), \\ \text{s.t.} \quad & g(x) \le 0, \\ & h(x) = 0. \end{split}\end{split}\]

Die vektorwertigen Funktionen \({g:\R^n\to\R^m}\) und \({h:\R^n\to\R^p}\) bilden dabei Nebenbedingungen, welche das Optimierungsproblem restringieren und als Gleichungen oder Ungleichungen auftreten können. Der Ausdruck s.t stammt dabei vom englischen subject to und wird in der deutschsprachigen Literatur auch häufig durch u.d.N (unter der Nebenbedingung) ersetzt.

Zur Veranschaulichung betrachten wir ein beschränktes, nichtlineares Optimierungsproblem.

Beispiel 3.1 (Beschränktes Optimierungsproblem)

Zwei Objekte bewegen sich auf elliptischen Orbits, beschrieben durch die Gleichungen

\[\begin{split}\begin{aligned} 1 &= \left(x-\tfrac{1}{5}\right)^2 + 2y^2 \quad \text{und}\\ \tfrac{1}{5} &= x^2 + xy + y^2. \end{aligned}\end{split}\]

Wir suchen die Positionen auf den jeweiligen Orbits, an denen die Objekte den geringsten Abstand zueinander haben.

Unseren Designsvektor \(x\in\R^4\) wählen wir dabei so, dass \((x_1,x_2)\) und \((x_3,x_4)\) jeweils die Position der beiden Objekte beschreiben. Die Zielfunktion lautet dann

\[\begin{split}f(x) = \frac{1}{2}\left\Vert \begin{pmatrix} x_1\\x_2\end{pmatrix}-\begin{pmatrix}x_3\\x_4\end{pmatrix}\right\Vert^2.\end{split}\]

Das Optimierungsproblem hat somit die Form

\[\begin{split}\begin{aligned} \min_{x\in\R^4}\quad & f(x), \\ \text{s.t.}\quad & \left(x_1-\tfrac{1}{5}\right)^2 + 2x_2^2 -1 = 0, \\ &x_3^2 + x_3x_4 + x_4^2 - \tfrac{1}{5} = 0. \end{aligned}\end{split}\]

Eine Illustration des Problems ist in Abb. 3.1 gegeben.

Bemerkung 3.1

Wir könnten zur Definition der Zielfunktion in Beispiel 3.1 anstelle von \({\tfrac{1}{2}\Vert\cdot\Vert^2}\) auch einfach \(\Vert\cdot\Vert\) verwenden. Das hätte allerdings den Nachteil, dass diese Funktion in 0 nicht differenzierbar ist. Wir werden im weiteren Verlauf der Vorlesung noch häufiger feststellen, dass Optimierung und Modellierung oft eng miteinander verbunden sind. Häufig gibt es mehr als eine Möglichkeit, ein Problem zu modellieren. Diese Möglichkeiten mögen zwar mathematisch äquivalent sein, sind im Allgemeinen aber nicht immer gleich nützlich.

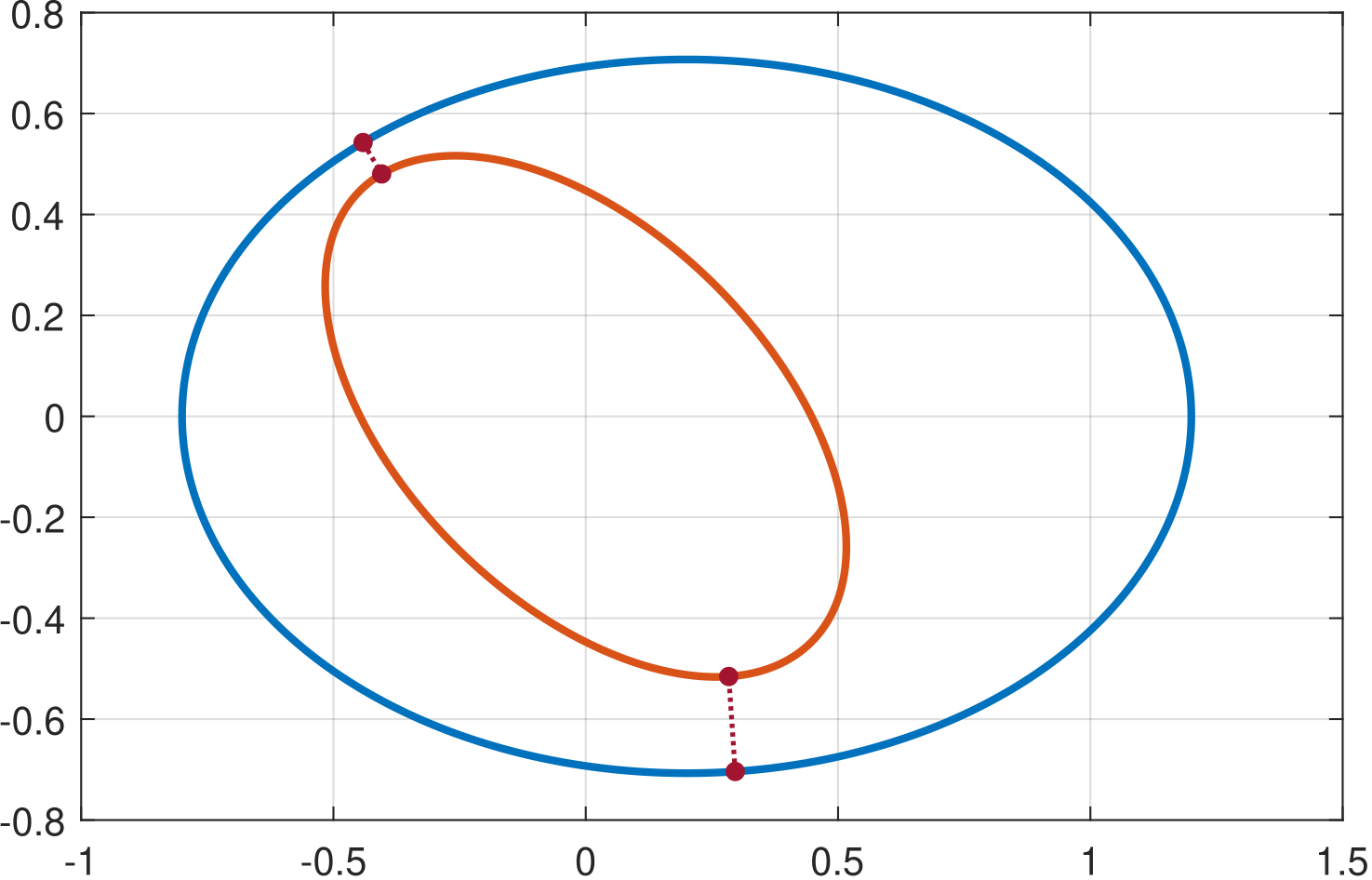
Abb. 3.1 Visualisierung des restringierten Optimierungsproblems in Beispiel 3.1. An zwei Stellen auf den jeweiligen Bahnen kommen sich die Objekte besonders nahe.

Wir stellen fest, dass es zwei Paare von Punkten gibt, an denen der Abstand (zumindest lokal) minimiert wird. Dementsprechend müssen wir uns wohl oder übel damit abfinden, dass Optimierungsprobleme im Allgemeinen keine eindeutige Lösung besitzen. Ebenso kann es passieren, dass ein Optimierungsproglem gar keine Lösung besitzt, z.B.

\[\min_{x\in\R}\quad e^{-x}.\]

Wir versuchen deshalb zunächst, unsere abstrakte Vorstellung eines Optimum formal zu beschreiben.

Definition 3.3 (Zulässigkeit, lokales und globales Minimum)

1. Die Menge

   \[X:=\left\{x\in\R^n\,:\, x\in\Omega,\; h(x)=0,\;g(x)\le 0 \right\}\subset\R^n\]

   heißt zulässiger Bereich für Problem (3.1).

2. Der Punkt \(x\in\R^n\) heißt zulässig für Problem (3.1), wenn \({x\in X}\).

3. Wir nennen \(x^\ast\in X\) ein lokales Minimum von (3.1), wenn es eine Umgebung \(U\subset X\) von \(x^\ast\in U\) gibt, so dass

   \[f(x^\ast) \le f(x)\quad\text{für alle }x\in U.\]

   Gibt es eine solche Umgebung, auf der sogar

   \[f(x^\ast) < f(x)\quad\text{für alle }x\in U\]

   gilt, dann nennen wir \(x^\ast\) striktes lokales Minimum.

4. Gilt \({f(x^\ast)\le f(x)}\) bzw. \({f(x^\ast)<f(x)}\) für alle \({x\in X}\), dann heißt \(x^\ast\) globales Minimum bzw. striktes globales Minimum von (3.1).

Bemerkung 3.2 (Äquivalenz von Minimierung und Maximierung)

In obiger Definition sprechen wir nur von Minima, jedoch ist klar, dass sich jedes Maximierungsproblem durch einen Vorzeichenwechsel leicht in ein Minimierungsproblem umformulieren lässt, d.h.,

\[\max_{x\in\Omega} f(x) \quad \Leftrightarrow \quad \min_{x\in\Omega} -f(x) \ =: \ \min_{x_\in\Omega} G(x).\]

Formal lassen sich folgende Gleichungen zeigen:

\[\begin{split}\begin{split} \max_{x\in\Omega} f(x) \ &= \ - \min_{x\in\Omega} -f(x),\\ \operatorname*{arg\,max}_{x\in\Omega} f(x) \ &= \ \operatorname*{arg\,min}_{x\in\Omega} -f(x). \end{split}\end{split}\]